Sampling Distributions of Sample Mean
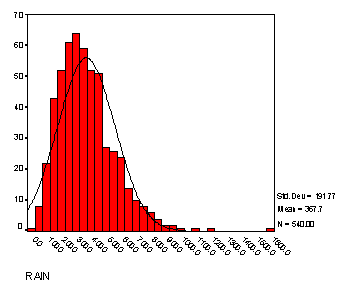
Philadelphia Rainfall Data
Population: 540 months of rainfall in Philadelphia (100ths of inches) from January, 1825-December, 1869.
Histogram with superimposed Normal curve:

Descriptive Statistics:
Descriptive Statistics
|
|
N |
Minimum |
Maximum |
Mean |
Std. Deviation |
|
RAIN |
540 |
19.00 |
1582.00 |
367.6796 |
191.77305 |
|
Valid N (listwise) |
540 |
|
|
|
|
Samples: Took 1000 random samples of size 30. Theoretical Mean and Standard Deviation (Standard Error) of Distribution of Sample Means:
![]()
Histogram of 1000 sample means (
n=30) with superimposed normal curve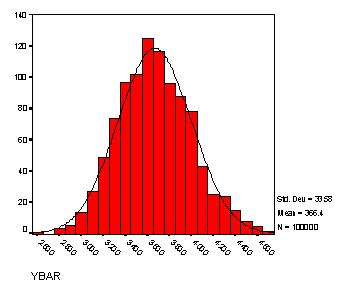
Descriptive Statistics:
Descriptive Statistics
|
|
N |
Minimum |
Maximum |
Mean |
Std. Deviation |
|
YBAR |
1000 |
259.10 |
469.30 |
366.4056 |
33.58160 |
|
Valid N (listwise) |
1000 |
|
|
|
|
Note: The mean of the sample means (366.41) is very close to the population mean (367.68). However, the standard deviation of the sample means (33.58) is further away, specifically below the theoretical standard deviation of the sampling distribution (35.0). This is (partly) due to the fact that we are sampling from a finite population, and that our sample size is relatively large as compared to the population size. When these sizes are known, we can incorporate the finite population correction factor for the standard deviation (standard error) of the sampling distribution of the sample mean:
![]()
Note that in practice, either the population size is unknown or or very large (even infinite), relative to the sample size, and this correction is ignored.